26.1 INTRODUCTION TO NEURAL NETWORKS

Neural network simulations seem to be a recent development . However, this field was established before the advent of computers . In fact, the first artificial neuron was produced in 1943 .

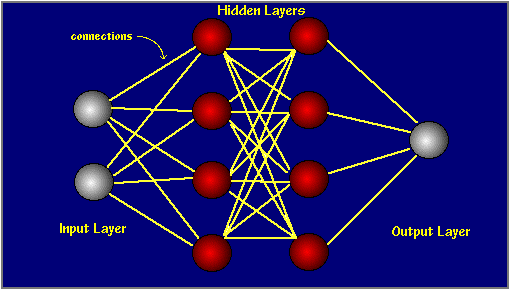
The designing of the first Artificial Neural Network ( ANN ) was inspired by the mechanism of similar biological nervous systems, such as the human brain . Artificial neurons with information processing abilities somewhat comparable to the human neuron were therefore made to suit this design . These neurons receive inputs from other sources, combine them in some way, perform a generally nonlinear operation on the result , and then output the final result . The neurons are typically organized in layers , each consisting of a large number of interconnected nodes . Data is presented to the network through the input layer , which communicates to one or more hidden layers where the actual processing is done by a system of weighted connections . These hidden layers then link to an output layer which produces the output .

Neural networks, with their remarkable ability to handle complicated data, can be used to detect and extract patterns that are too complex to be noticed by either humans or other computer techniques . A well trained neural network can be thought of as an expert in the field of information it has been trained to analyse .

Many experiments were carried out to determine the capabilities of these networks . In one of these experiments, an ANN was put in control of a moving vehicle to compare human driving behavior with that of the neural network . The results showed a surprising similarity between both . According to the experiment, neural networks can behave with a maximum error of 5 % .

Over all, the future of neural networks seems to be promising considering the variety of tasks it can handle as we will see later .

The exact workings of the human brain are still a mystery. Yet, some aspects of this amazing processor are known. In particular, the most basic element of the human brain is a specific type of cell which, unlike the rest of the body, doesn't appear to regenerate. Because this type of cell is the only part of the body that isn't slowly replaced, it is assumed that these cells are what provides us with our abilities to remember, think, and apply previous experiences to our every action. These cells, all 100 billion of them, are known as neurons. Each of these neurons can connect with up to 200,000 other neurons, although 1,000 to 10,000 is typical. Neurons are wired up in a three-dimensional pattern.

In the human brain, a typical neuron collects signals from others through a host of fine structures called dendrites. The neuron sends out spikes of electrical activity through a long, thin strand known as an axon, which splits into thousands of branches.

At the end of each branch, a structure called a synapse converts the activity from the axon into electrical effects that inhibit or excite activity in the connected neurones. When a neuron receives excitatory input that is sufficiently large compared with its inhibitory input, it sends a spike of electrical activity down its axon. Learning occurs by changing the effectiveness of the synapses so that the influence of one neuron on another changes.

The power of the human mind comes from the sheer numbers of these basic components and the multiple connections between them. It also comes from genetic programming and learning.

The individual neurons are complicated. There are over one hundred different classes of neurons, depending on the classification method used. Together these neurons and their connections form a process which is not binary, not stable, and not synchronous. In short, it is nothing like the currently available electronic computers, or even artificial neural networks.

The understanding of the biological neuron’s method in processing and transferring information led the way to the design of the artificial neuron . This artificial neuron is considered the building block of a neural network . It was made to function the same way the biological one does. It takes many inputs having different weightings and has one output which depends on the inputs.

The artificial neuron has two modes of operation; the ‘training mode’ and the ‘using mode’. In the training mode, the neuron can be trained to fire (or not), for particular input patterns. In the using mode, when a taught input pattern is detected at the input, its associated output becomes the current output.

A biological neuron can either 'fire' or not 'fire'(When a neuron fires, it outputs a pulse signal of a few hundred Hz). In an artificial neuron 'firing' is normally represented by a logical one and ‘not firing’ by a logical zero.

Fig 26-4 A basic artificial neuron

In the above figure , various inputs to the network are represented by the

mathematical symbol, x(n). Each of these inputs are multiplied by a connection weight. These weights are represented by w(n). In the simplest case, these products are simply summed, fed through a transfer function to generate a result, and then output. This process lends itself to physical implementation on a large scale in a small package. This electronic implementation is still possible with other network structures which

utilize different summing functions as well as different transfer functions.

Although artificial neural networks process information in a similar way the human brain does, real brains, however, are orders of magnitude more complex than any artificial neural network so far considered.

Neural networks take a different approach to problem solving than that of

conventional computers. Conventional computers use an algorithmic approach

i.e., the computer follows a set of instructions in order to solve a problem. Unless the specific steps that the computer needs to follow are known , the computer cannot solve the problem. That restricts the problem solving capability of conventional computers to problems that we already understand and know how to solve. But computers would be so much more useful if they could do things that we don't exactly know how to do.

Neural networks process information in a similar way the human brain does . The network is composed of a large number of highly interconnected processing elements(neurons) working in parallel to solve a specific problem. Neural networks learn by example. They cannot be programmed to perform a specific task. The examples must be selected carefully otherwise useful time is wasted or even worse the network might be functioning incorrectly. The disadvantage is that because the network finds out how to solve the problem by itself, its operation can be unpredictable.

On the other hand, conventional computers use a cognitive approach to problem solving; the way the problem is to be solved must be known and stated in small unambiguous instructions. These instructions are then converted to a high level language program and then into machine code that the computer can understand. These machines are totally predictable; if anything goes wrong is due to a software or hardware fault.

Neural networks are a form of multiprocessor computer system, with:

* simple processing elements

* a high degree of interconnection

* simple scalar messages

* adaptive interaction between elements

Neural networks and conventional algorithmic compare not in competition but complement each other. There are tasks that are more suited to

conventional computers like arithmetic operations , and tasks that are more suited to neural networks. Even more, a large number of tasks, require systems that use a combination of the two approaches (normally a conventional computer is used to supervise the neural network) in order to perform at maximum efficiency.

Neural networks do not perform miracles. But if used sensibly they can produce some amazing results.

As mentioned earlier, The commonest type of artificial neural network consists of three layers of units: a layer of input units is connected to a layer of hidden units which is connected to a layer of output units. Depending on the connections between these layers, neural networks can be either feed-forward or feedback networks.

Feed-forward networks allow signals to travel one way only; from input to output. There is no feedback (loops) i.e., the output of any layer does not affect that same layer. Feed-forward networks tend to be straight forward types of networks that associate inputs with outputs. They are extensively used in pattern recognition.

Feedback networks can have signals travelling in both directions by introducing loops in the network. They are very powerful and can get extremely complicated. Feedback networks are dynamic, their state is changing continuously until they reach an equilibrium point. They remain at the equilibrium point until the input changes and a new equilibrium needs to be found.

The weights between the input and hidden layers determine when each hidden unit is active and what it represents, and so determining the output of these units.

26.2.2 The Firing Rule

The firing rule is an important concept in neural networks and accounts for their high flexibility. A firing rule determines how one calculates whether or not a neuron should fire for any input pattern. It relates to all the input patterns, not only the ones on which the node was trained. If a pattern is received during the execution stage that is not associated with an output, the neuron selects the output that corresponds to the pattern from the set of patterns that it has been taught of, that is least different from the input. This is called generalisation.

For example:

A 4-input neuron is trained to fire when the input is 1111 and not to fire when the input is 0000. After applying the generalisation rule the neuron will also fire when the input is 0111, 1011, 1101, 1110 or 1111 but will not fire when the input is 0000, 0001, 0010, 0100 or 1000. Any other inputs (like 0011) will produce a random output since they are equally distant from 0000 and 1111 .

Therefore the firing rule enables the neuron to respond sensibly to patterns it has not seen during training.

Every neural network possesses knowledge which is contained in the values of the connections’ weights.Learning is the process of determination of these weights and modifying them according to the experience the network is subjected to.Following the way learning is performed,we can distinguish two major categories of neural networks:

[i] Fixed networks : in which the weights cannot be changed, i.e.,dw/dt = 0.In such networks,the weights are fixed according to the problem to be solved.

[ii] Adaptive networks : which are able to change their weights, i.e.,dw/dt ¹ 0.

All learning methods used for adaptive neural networks can be classified into two major categories:

[1] Supervised learning which requires an external teacher,so that each output unit is told what its desired response to input signals ought to be.Paradigms of supervised learning include error correction learning, reinforcement learning and stochastic learning.An important issue concerning supervised learning is the problem of error convergence, i.e., the minimization of error between the desired and computed unit values.The aim is to determine a set of weights which minimizes the error.One well-known method, which is common to many learning paradigms is the least mean square (LMS) convergence.

[2] Unsupervised learning which uses no external teacher and is based upon only local information. It is also referred to as self-organization, in the sense that it self-organizes data presented to the network and detects their emergent collective properties. Paradigms of unsupervised learning are Hebbian learning and competitive learning.

An unsupervised learning algorithm might emphasize co-operation among clusters of processing elements.In such a scheme,the clusters would work together.If some external input activated any node in the cluster,the cluster’s activity as a whole could be increased.Likewise,if external input to nodes in the cluster was decreased,that could have an inhibitory effect on the entire cluster.

Competition between processing elements could also form a basis for learning.Training of competitive clusters amplify the responses of specific groups to specific stimuli.As such,it would associate those groups with each other and with a specific appropriate response. Normally,when competition for learning is in effect,only the weights belonging to the winning processing element will be updated.

We say that a neural network learns ‘off-line’ if the learning phase and the operation phase are distinct. A neural network learns ‘on-line’ if it learns and operates at the same time. Usually, supervised learning is performed off-line, whereas unsupervised learning is performed on-line.

• Learning Rates

The rate at which artificial neural networks learn depends upon several controllable factors.Time is one of these factors and is considered the most important one. Obviously,a slower rate means that more time is spent in accomplishing the off-line learning to produce an adequately trained system.With the faster learning rates, however,the network may not be able to make the fine discriminations possible with a system that learns more slowly.Researchers are working on producing the best of both worlds. There are other factors that affects the learning rates.From these factors we mention network complexity , size , paradigm selection and architecture , type of learning and the desired accuracy.

• Learning Laws

Many learning laws are in common use. Most of these laws are some sort of

variation of the best known and oldest learning law, Hebb's Rule. Learning is certainly more complex than the simplifications represented by the learning laws currently developed. In the following lines we introduce some of the major learning laws:

Hebb's Rule: The first, and undoubtedly the best known, learning rule was introduced by Donald Hebb. His basic rule is: “ If a neuron receives an input from another neuron, and if both are highly active (mathematically have the same sign), the weight between the neurons should be strengthened.”

Hopfield Law: It is similar to Hebb's rule with the exception that it specifies the magnitude of the strengthening or weakening. It states, “ if the desired output and the input are both active or both inactive,increment the connection weight by the learning rate, otherwise decrement the weight by the learning rate.”

The Delta Rule: This rule is a further variation of Hebb's Rule. It is one of the most commonly used. This rule is based on the simple idea of continuously modifying the strengths of the input connections to reduce the difference (the delta) between the desired output value and the actual output of a processing element. This rule changes the synaptic weights in the way that minimizes the mean squared error of the network. This rule is also referred to as the ‘Widrow-Hoff Learning Rule’ and the ‘Least Mean Square’(LMS) Learning Rule.The way that the Delta Rule works is that the delta error in the output layer is transformed by the derivative of the transfer function and is then used in the previous neural layer to adjust input connection weights. In other words, this error is bacpropagated into previous layers, one layer at a time. The process of back-propagating the network errors continues until the first layer is reached. The network type called Feedforward, Back-propagation derives its name from this method of computing the error term.When using the delta rule, it is important to ensure that the input data set is well randomized. Well ordered or structured presentation of the training set can lead to a network which can not converge to the desired accuracy. If that happens, then the network is incapable of learning the problem.

The Back-propagation algorithm will be discussed in details in section 26.2.4.

The Gradient Descent Rule: This rule is similar to the Delta Rule in that the derivative of the transfer function is still used to modify the delta error before it is applied to the connection weights. Here, however, an additional proportional constant tied to the learning rate is appended to the final modifying factor acting upon the weight. This rule is commonly used, even though it converges to a point of stability very slowly.

It has been shown that different learning rates for different layers of a network help the learning process converge faster. In these tests, the learning rates for those layers close to the output were set lower than those layers near the input. This is especially important for applications where the input data is not derived from a strong underlying model.

Kohonen's Learning Law: This procedure, developed by Teuvo Kohonen, was

inspired by learning in biological systems. In this procedure, the processing elements compete for the opportunity to learn, or update their weights. The processing element with the largest output is declared the winner and has the capability of inhibiting its competitors as well as exciting its neighbors.Only the winner is permitted an output, and only the winner plus its neighbors are allowed to adjust their connection weights.

Further, the size of the neighborhood can vary during the training period.The usual paradigm is to start with a larger definition of the neighborhood, and narrow in as the training process proceeds. Because the winning element is defined as the one that has the closest match to the input pattern, Kohonen networks model the distribution of the inputs. This is good for statistical or topological modeling of the data and is sometimes referred to as self-organizing maps or self-organizing topologies.

The back-propagation algorithm has become nowadays one of the most important tools for training neural networks .In order to train a neural network to perform some task, we must adjust the weights of each unit in such a way that the error between the desired output and the actual output is reduced. This process requires that the neural network compute the error derivative of the weights (EW). In other words, it must calculate how the error changes as each weight is increased or decreased slightly. The back propagation algorithm is the most widely used method for determining the EW.

This method is easier to understand if all the units in the network are linear. The algorithm computes each EW by first computing the EA, the rate at which the error changes as the activity level of a unit is changed. For output units, the EA is simply the difference between the actual and the desired output. To compute the EA for a hidden unit in the layer just before the output layer, we first identify all the weights between that hidden unit and the output units to which it is connected. We then multiply those weights by the EAs of those output units and add the products. This sum equals the EA for the chosen hidden unit. After calculating all the EAs in the hidden layer just before the output layer, we can compute in like fashion the EAs for other layers, moving from layer to layer in a direction opposite to the way activities propagate through the network. This is what gives back propagation its name. Once the EA has been computed for a unit, it is straight forward to compute the EW for each

incoming connection of the unit. The EW is the product of the EA and the activity through the incoming connection.

Note that for non-linear units, the back-propagation algorithm includes an extra step. Before back-propagating, the EA must be converted into the EI, the rate at which the error changes as the total input received by a unit is changed.

Neural networks are universal approximators.They work best if the system we are using them to model has a high tolerance to error or when the relationships between variables are hardly understood or when the relationships are difficult to describe adequately with conventional approaches.In this section,we introduce some applications in which neural networks are being used.

Monitoring: Neural networks have been used to monitor

* the state of aircraft engines. By monitoring vibration levels and sound, early warning of engine problems can be given.

* British Rail have also been testing a similar application monitoring diesel engines.

Investment Analysis: To attempt to predict the movement of stocks currencies etc., from previous data. There, they are replacing earlier simpler linear models.

Medicine: Artificial Neural Networks (ANN) are currently a 'hot' research area in

medicine and it is believed that they will receive extensive application to biomedical systems in the next few years. At the moment, the research is mostly on modeling parts of the human body and recognizing diseases from various scans (e.g. cardiograms, CAT scans, ultrasonic scans, etc.).Neural networks learn by example so the details of how to recognize the disease are not needed. What is needed is a set of examples that are representative of all the variations of the disease. The quantity of examples is not as important as the 'quantity'. The examples need to be selected very carefully if the system is to perform reliably and efficiently.Here are some medical applications of ANNs:

Neural Networks are used experimentally to model the human cardiovascular system. Diagnosis can be achieved by building a model of the cardiovascular system of an individual and comparing it with the real time physiological measurements taken from the patient. If this routine is carried out regularly, potential harmful medical conditions can be detected at an early stage and thus make the process of combating the disease much easier.A model of an individual's cardiovascular system must mimic the

relationship among physiological variables (i.e., heart rate, systolic and diastolic blood pressures, and breathing rate) at different physical activity levels. If a model is adapted to an individual, then it becomes a model of the physical condition of that individual. The simulator will have to be able to adapt to the features of any individual without the

supervision of an expert. This calls for a neural network.

ANN are used experimentally to implement electronic noses. Electronic noses have several potential applications in telemedicine.Telemedicine is the practice of medicine over long distances using a communication link. The electronic nose would identify

odours in the remote surgical environment.These identified odours would then be electronically transmitted to another site where an odour generation system would

recreate them. Because the sense of smell can be an important sense to the surgeon, telesmell would enhance telepresent surgery.

Language Processing: Language processing includes a wide variety of applications. These applications include text-to-speech conversion, auditory input for machines, automatic language translation, secure voice keyed locks,automatic transcription, aids for the deaf, aids for the physically disabled which respond to voice commands, and natural language processing.One of the most important recent researches is how a computer, via ANN, could be programmed to respond to spoken commands.This requires an ANN that can understand the 50,0most commonly spoken words.

Image (data) Compression: A number of studies have been done proving that neural networks can do real-time compression and decompression of data. These networks are auto associative in that they can reduce eight bits of data to three and then reverse that process upon restructuring to eight bits again. However, they are not lossless. Because of this losing of bits they do not favorably compete with more traditional methods.

Servo Control: Controlling complicated systems is one of the more promising areas of

neural networks. Most conventional control systems depend on some parameters.To customize a system for a specific process, those parameters must be manually tuned to reach a combination that produces the desired results.On the other hand,neural networks offer the advantage that they learn on their own.They don't require control

system's experts, just simply enough historical data so that they can train themselves.

NASA is working on a system to control the shuttle during in-flight maneuvers. This system is known as Martingale's Parametric Avalanche.Another prototype application is known as ALVINN, for Autonomous Land Vehicle in a Neural Network. This project has mounted a camera and a laser range finder on the roof of a vehicle which is being taught to stay in the middle of a winding road.

British Columbia Hydroelectric funded a prototype network to control operations of a power-distribution substation that was so successful at optimizing four large synchronous condensors that it refused to let its supplier, Neural Systems, take it out.

It is one of the first large scale applications of artificial neural networks.It is the process of verifying the writer's identity by checking the signature against samples kept in a database. The result of this process is usually a number between 0 and 1 which represents a fit ratio (1 for match and 0 for mismatch). The threshold used for confirmation / rejection decision depends on the nature of the application. The aim of this analysis is to develop a signature verification system based on very low end processors, suitable for commercial use. It is essential for these applications to keep both the computing complexity and the data amount used for verification as small as possible. The small data size is very important for fast data transfers in network

applications and/or cheap digital storage on personal cards. The time for checking the new signature is critical because this is the time seen by the user. However, the

learning time is less important since the training for one person occurs only once.

A signature verification system has five components:

(1) Data capture: the process of converting the signature into digital form.

(2) Preprocessing: the data transformation in a standard format.

(3) Feature extraction: the process of extracting key information from the digital

representation of the signature.

(4) Comparison process: matches extracted features with templates stored in a

database. Usually, the output is a fit ratio.

(5) Performance evaluation: the decision step typically made by thresholding the fit

value.

An example of signature verification systems is shown in the following implementation:

* Data capture is done with a touch panel and an 8-bit ADC (analog-to-digital converter) with a resolution in the 25-100 dpi range.

* Feature extraction is based on a proprietary method. The selected features are represented by a string of 128 bytes size and rotation invariant.

* The comparison is implemented as a neural network which has as output a real

number between 0 and 1. Usually a genuine signature scores above 0.90-0.95, variable from signer to signer. The needed data for checking are the weights of synapses of the neural network. The topology is proprietary and reduces the data stored to less than 350

bytes. A method to train the network (a back-propagation neural network was used for tests) for each person was also developed.

Test Results:

The algorithm was tested with over 10 different people. The neural network was able to learn and identify all signatures.A number of 4 to 6 samples were presented as good signatures for training.A small number is convenient from the user interface point of view. As the number of samples grows the accuracy of the algorithm increases. The

learning time on a Pentium/100 was between 2 and 25 seconds. The feed-forward time (the time needed to test a signature) is less than 47 micro seconds.The accuracy can be improved also by using some false signatures for training (i.e. presenting forgeries as learning data). In these tests only genuine samples were used.

The trained network was tested with other signatures. All the genuine signatures scored above 0.9 match; the fake ones (somebody signed as another person) were scored under 0.7, so the distance between the good signatures and the forgeries is clear.

Character recognition is a process which converts a graphical character into its textual counterpart. Humans perform this operation as they read, taking the printed character, interpreting its shape, and assigning meaning. Computers cannot normally achieve this intelligence and instead must be taught how to recover text from a character image.There are two methods for performing character recognition:

template based and feature based recognition. While there are hundreds of different

algorithms for each of these methods, the principle behind the particular algorithm falls into one of these two categories.

Template based recognition: matches each input character image against a library of known character images called ‘templates’. These templates are images themselves, and graphically represent a known character. The input image is compared to each of the templates and a value corresponding to the similarity between the two images is computed. The highest value corresponds to the input character.

Note: If the input is not in the library, the highest value corresponds to the image in the library that is most similar to the input character.

Template based recognition schemes can be very effective when only few fonts are used in the text to be translated.Templates must be constructed for all possible permutations of each character so that an accurate matching value can be computed. The accuracy of a template based recognition system depends on some factors such as the quality of the input images, number of templates, and orientation of the characters. All input images must be scaled, translated, and rotated to match the size and orientation of the template images.

Feature based recognition: attempts to determine which character is being portrayed by examining the particular strokes that make up that image. For example, an 'H' has two vertical lines of approximately equal length, one horizontal line, and two T-intersections. These features are compared to a list of features common to each possible character. The input is identified as the character whose features best match that of the input image. Feature based recognition systems are applicable in situations where many different fonts are present in the text or the orientation of the text cannot be controlled. In these cases, analysis of the shape of the character may be necessary to accurately recognize each character.

The largest amount of research in the field of character recognition is aimed at scanning oriental characters into a computer.In practical life,character recognition has been successfully used in many applications.One of these applications is a neural network based product that can recognize hand printed characters through a scanner. This product can take cards, like a credit card application form, and put those

recognized characters into a data base. It is 98% to 99% accurate for numbers, a little

less for alphabetical characters. This product is being used by banks, financial institutions, and credit card companies.Another application is a software package that is capable of recognizing characters,including cursive.It has proven successful in analyzing reasonably good handwriting.

Now, we introduce some applications related to the concept of character recognition

provided with some examples.

In character recognition, the general rules for distinguishing between characters are neither known,nor have they been formulated.The best current process is to examine a large cross section of the character population with the goal of finding a function that adequately generalizes the exemplars from the training set.This would possibly allow for recognition of the test characters not contained in the original training set. Let us look at an example: a project for handwritten digit recognition.Typical digit examples used for this project are shown in Figure 26-5.The digits are written by many different people using a great variety of sizes,writing styles,instruments,and with a widely varying amount of care.It can be noted that many of the digits are poorly formed and are hard to classify,even for a human.The captured digits are first normalized to fill an area consisting of 40 x 60 black and white pixels.The resulting normalized patterns are presented to a neural network after being reduced to 16 x 16 pixel images.Further processing is performed by a mix of custom hardware and specialized software for image processing .

Skeletonization is a process that makes the lines one dimensional by removing meaningless linewidth variations.The rationale for line-thinning preprocessing is that a smaller number of features is sufficient to analyze the skeletonized images.Since the linewidth does not carry much information about the character itself, the skeletonization removes pixels of the image until only a backbone of the character remains,and the broad strokes are reduced to thin lines.Skeletonization is illustrated in Figure 26-6(a) where the gray area represents the original character,the digit 3, and the black area is its skeletonized image.

The skeletonization is implemented through scanning of the 5 x 5 pixel window template across the entire image.Twenty different 25-bit window templates are stored on the neural network chip.These templates are responsible for performing the skeletonization of the images.One of the templates is shown in Figure 26-6(b).During scanning each template tests for a particular condition that allows the deletion of the middle pixel in the window. If the match of the image pixels to any of the templates exceeds a preset threshold value, the center pixel of the character bit map is deleted.

In this manner, the entire 16 x 16 pixel image is scanned, and a decision is made for each pixel in the image whether that pixel just makes the line fat and can be deleted, or whether its presence is crucial to keep the connectivity of the character intact.

Examples of a single scanning pass through the image using four selected window templates are shown in Figure 26-7.The black pixels deleted in the images shown as a result of each template pass are marked in gray on the four images in each box.

The skeletonization process is followed by the feature extraction process for each character. In the feature extraction stage, the thinned image is presented to a number of 7 x 7 feature extracting pixel window templates. The neural network chip stores 20 different feature extracting window templates. Feature extraction processing by means of window templates is illustrated in Figure 26-8. The templates check for the presence of oriented lines, oriented line ends, and arcs in the image of a skeletonized character, for example, like the one displayed in Figure 26-8(a). Examples of the extracted features of line endstops and horizontal lines are shown in Figures 26-8

(b),(c),and (d).Whenever a feature template match exceeds the preset threshold, a 1 is set in a blank feature map for that corresponding feature. In this way, a feature map is produced for every template. The maps of such features for each evaluated character skeleton are then subjected to an “OR” function after the scan is completed .

The feature extraction process terminates by mapping the skeletonized input pattern of 16 x 16 size image into 20 different 16 x 16 feature images. To compress the data, each feature map is then coarse-blocked into a 3 x 3 array. As a final result of processing for feature extraction, 20 different 3 x 3 feature vectors, consisting jointly of 180 feature entries, are produced.These entries are then classified into one of the 10 categories signifying each of the 10 digits.

The multilayer feedforward neural network for handwritten character recognition can be directly fed with images obtained as slightly preprocessed original patterns containing low-level information. First, the 40 x 60 pixel binary input patterns are transformed to fit into a 16 x 16 pixel frame using a linear transformation . This frame contains the target image. The transformation preserves the aspect ratio of the character, but the resulting target image consisting of 256 entries is not binary. It has multiple gray levels because a variable number of pixels in the original input pattern can fall into a given pixel of the target image. The gray levels of each resulting target

image are then scaled and translated to fall within the bipolar neuron’s output value range, - 1 to +1. This step is needed to utilize fully the mapping property of the activation function of the first layer of neurons.

The remainder of the recognition processing is performed by a rather elaborate multilayer feedforward network trained using the error back-propagation technique. The architecture of the network is shown in Figure 26-9. The network has three hidden layers, J1, J2, and J3, and an output layer consisting of 10 neurons.The hidden layers perform as trainable feature detectors.

The first hidden layer denoted as J1 consists of 12 groups of 64 units per group, each arranged in an 8 x 8 square. Each unit in J1 has connections only from the

(25 + 1), from the @ 200 000 that would be needed for a fully connected first hidden layer. Due to the weight sharing, only 768 biases and 300 weights remain as free parameters of this layer during training.

The second hidden layer uses a similar set of trainable feature detectors consisting of 12 groups of 16 units, again taking input from 5 x 5 receptive fields. A 50% reduction of image size and weight sharing take place in this layer. The connection scheme is quite similar to the first input layer; however, one slight complication is due to the fact that J1 consists of multiple two-dimensional maps. Inputs to J2 are taken from 8 of the 12 groups in J1. This makes a total of 8 x 25 shared weights per single group in J2. Thus, every unit in J2 has 200 weights and a single bias. Since this J2 layer consists of 192 units, it employs 38 592 (192 x 201) connections. All these connections are controlled by only 2592 free trainable parameters. Twelve feature maps

of tlayer involve 200 distinct weights each, plus the total of 192 thresholds.

Layer J3 has 30 units and is fully connected to the outputs of all units in layer J2. The 10 output units are also fully connected to the outputs of layer J3. Thus, layer J3 contains 5790 distinct weights consisting of 30 x 192 units plus 30 thresholds. The output layer adds another 310 weights, of which 10 are thresholds of output neurons.

The overall throughput rate of the complete, trained digit recognizer, including the image acquisition time, is reported to be 10 to 12 digit classification per second.

An important application of neural networks is pattern recognition. A pattern is the quantitative description of an object, event, or phenomenon. There are two kinds of patterns, spatial and temporal patterns. Spatial patterns include pictures, video images, weather maps, and fingerprints. Temporal patterns usually involve data appearing in time, such as speech signals, electrocardiograms, and signals versus time outputs produced by sensors. The goal of pattern recognition is to recognize and assign input patterns to specified categories. Pattern recognition can be implemented by using a feed-forward neural network that has been trained accordingly. The following figure shows the block diagram of the recognition and classification system.

The classifying system consists of an input transducer providing the input pattern data to the system. The feature extractor then receives its input as sets of data vectors that belong to a certain category. Usually this converted data can be compressed while still maintaining the same level of machine performance. The compressed data are called features. The feature extractor is responsible for performing this reduction of dimensionality. Therefore, the dimensionality of the feature space(output of feature extractor) is assumed to be much smaller than the dimensionality of the pattern space(input to feature extractor). The feature vectors retain the minimum number of data dimensions while maintaining the probability of correct classification, thus making handling data easier.

During training, the network is trained to associate outputs with input patterns. The power of neural networks comes to life when a pattern that has no output associated with it, is given as an input. In this case, the network gives the output that corresponds to a taught input pattern that is least different from the given pattern. .

For example:

The network in the following figure is trained to recognize the patterns T and H. The associated patterns are all black and all white respectively as shown below.

If we represent black squares with 0 and white squares with 1 then the truth tables for the 3 neurons after generalization are;

X11: 0 0 0 0 1 1 1 1

X12: 0 0 1 1 0 0 1 1

X13: 0 1 0 1 0 1 0 1

OUT: 0 0 1 1 0 0 1 1

Top neuron

X21: 0 0 0 0 1 1 1 1

X22: 0 0 1 1 0 0 1 1

X23: 0 1 0 1 0 1 0 1

OUT: 1 0/1 1 0/1 0/1 0 0/1 0

Middle neuron

X31: 0 0 0 0 1 1 1 1

X32: 0 0 1 1 0 0 1 1

X33: 0 1 0 1 0 1 0 1

OUT: 1 0 1 1 0 0 1 0

Bottom neuron

From the tables it can be seen the following associations can be extracted:

In this case, it is obvious that the output should be all blacks since the input pattern is almost the same as the 'T' pattern.

Here also, it is obvious that the output should be all whites since the input pattern is almost the same as the 'H' pattern.

Here, the top row is 2 errors away from a T and 3 from an H. So the top output is black. The middle row is 1 error away from both T and H so the output is random. The bottom row is 1 error away from T and 2 away from H. Therefore the output is black. The total output of the network is still in favour of the T shape.

The previous neuron doesn't do anything that conventional computers cannot do using algorithm. But a more complicated neuron , the McCulloch and Pitts model (MCP), weights the inputs which means that the effect that each input has at decision making is dependent on the weight of the particular input. The weight of an input is a number which when multiplied with the input gives the weighted input. These weighted inputs are then added together and if they exceed a pre-set threshold value, the neuron fires. In any other case the neuron does not fire. In mathematical terms, the neuron fires if and only if;

X1W1 + X2W2 + X3W3 + ... > T

The addition of input weights and of the threshold makes this neuron a very flexible and powerful one. The MCP neuron has the ability to adapt to a particular situation by changing its weights, or threshold, or both. Various algorithms exist that cause the neuron to 'adapt'. The most widely used ones are the Delta rule for feed-forward networks and the back error propagation for feedback networks.

Recently, a number of pattern recognition applications have been published. One application is a system that can detect bombs in luggage at airports by identifying, from small variances, patterns from within specialized sensor's outputs. Another article reported how a physician had trained a back-propagation neural network to collect data from people in emergency rooms who felt that they were experiencing a heart attack to provide the probability of a real heart attack versus a false alarm. This system has proved to be a very good discriminator in areas where priority decisions have to be made all the time.

Another application involves the grading of rare coins. Digitized images from an electronic camera are fed into a neural network. These images include several angles of the front and back. These images are then compared against known patterns which represent the various grades for a coin. This system makes a quick evaluation for about $15 compared to the standard three-person evaluation which costs $200. The results have shown that the neural network recommendations are as accurate as the people-intensive grading method. Yet, the biggest use of neural networks as a recognizer of patterns is in the field of quality control. Many automated quality applications are now in use. These applications aim to find that one in a hundred (or even one in a thousand) part that is defective. Human inspectors become tired or sometimes distracted. Systems now evaluate solder joints, welds, cuttings, and glue applications. One car manufacturer is now even prototyping a system which digitizes pictures of new batches of paint to determine if they are the right shades.

Another major area of applications for pattern recognition systems is as processors for sensors. Sensors can provide so much data that the few meaningful pieces of information can become lost. People can lose interest as they stare at screens looking for "the needle in the haystack." Many of these sensor-processing applications are used in defense industry. Neural network systems have been proven to be successful at recognizing targets. These sensor processors take data from cameras, sonar systems, seismic recorders, and infrared sensors. That data is then used to identify a probable phenomenon.

Recognition of patterns within the sensor data of the medical industry is related also to the defense sensor processi. A neural network is now being used in the scanning of PAP smears. This network is trying to do a better job at reading the smears than the average lab technician. In medical industry, there is a common problem of missed diagnoses. In many cases, a professional must perceive patterns from noise, such as identifying a fracture from an X-ray. Neural networks promise, particularly when faster hardware becomes available, help in many areas of the medical profession where data is hard to read.

The computing world has a lot to gain fron neural networks. Their ability

to learn by example makes them very flexible and powerful. Furthermore there is no need to devise an algorithm in order to perform a specific task; i.e. there is no need to understand the internal mechanisms of that task. They are also very well suited for real time systems because of their fast responseand computational times which are due to their parallel architecture.

Neural networks also contribute to other areas of research such as neurology and psychology. They are regularly used to model parts of living organisms and to investigate the internal mechanisms of the brain.

Perhaps the most exciting aspect of neural networks is the possibility that

some day 'consious' networks might be produced. There is a number of scientists arguing that conciousness is a 'mechanical' property and that 'consious' neural networks are a realistic possibility.

Finally, I would like to state that even though neural networks have a huge

potential we will only get the best of them when they are intergrated with computing, AI, fuzzy logic and related subjects.